English version   versión Española

Introduction

    Dans ce qui suit, je vais utiliser le lien qui existe entre la taille et la quantité de chaleur échangée par un objet pour expliquer des phénomènes que vous avez pu observer comme le fait qu'un enfant se refroidit plus vite qu'un adulte. Le fil conducteur sera de répondre à la question : pourquoi un enfant ne transpire pas en faisant un effort physique, contrairement à un adulte (ceci, sous certaines contraintes qu'on évoquera plus loin (même quantité de chaleur produite par l'effort <> même effort physique (vitesse identique) car masse ~h³)).
    Pour mieux comprendre les notions expliquées dans la suite, rien ne vaut l'expérimentation. Je vous conseille donc vivement de vous procurer des jeux pour enfants tels que des cubes ou des briques de construction en plastique avant de plonger dans ce document.
    La difficulté des notions est indiquée par des symboles et se répartie entre débutant, averti et initié. N'h"sitez pas à parcourir les paragraphes plus difficils, vous y trouverez toujours quelques informations utiles à glanner.

    Commençons par voir quel est l'influence de la taille sur un objet. Pour cela nous pourrions prendre une sphère (comme dans un autre document), mais pour aider à la compréhension, je vais choisir un pavé rectangulaire

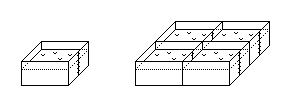
    Considérons un pavé qui nous servira d'étalon. On souhaite, par exemple, obtenir un pavé "deux fois plus gros", au sens que toutes ses arêtes soient deux fois plus longues.

    Si ses arêtes font a, b et c de longueur, alors le nouveau pavé aura des arêtes de longueur 2a, 2b et 2c. Par extension, toute distance entre deux points quelconques sera deux fois plus grande; un point situé au milieu de l'arête verticale est à c/2 (respectivement c) des sommets les plus proches.

    A l'aide de la relation de Pythagore, il n'est pas difficile de s'en rendre compte. Par exemple, la distance entre deux sommets les plus éloignés (ils sont situés sur la diagonale) est, (a²+b²+c²)^1/2 pour le pavé étalon et devient (4a²+4b²+4c²)^1/2 dans le second cas. Il y a donc bien un facteur deux entre ces distances.
    Ce facteur est le nombre de fois qu'il faut reporter le pavé pour obtenir la taille voulue.

    ii Surface

    Procédons de la même manière pour obtenir le facteur qui lie les surfaces du grand pavé au pavé étalon; comblons chaque face et comptons le nombre de faces utilisées.

    On constate que chaque face a pour aire le quadruple de la face initiale. C'est normal puisque la surface d'un rectangle est le produit de deux longueurs; si celles-ci sont agrandies du même facteur, alors la surface augmente du carré de ce facteur.

    iii Volume

    Si vous avez compris le processus jusqu'à maintenant, alors vous avez certainement déjà trouvé la solution pour le volume.

    Le grand pavé est formé de huit pavés étalons, d'où le volume est :

    iv Généralisation : facteur d'échelle

    Ce raisonnement n'est pas propre qu'à un doublement des dimensions; il est aussi valable pour un agrandissement triple, quadruple, etc. Cela marche aussi pour une réduction ou pour des facteurs non entiers. Si h est ce facteur d'échelle, alors on a en général :

Ainsi, si deux objets diffèrent par la taille mais pas la forme, alors leurs grandeurs spatiales seront dans ces proportions.
Un enfant et un adulte sont deux tels objets. Leurs tailles diffèrent, mais leurs formes, à quelques approximations près, sont identiques; un adulte n'est pas la version étirée d'un enfant et à l'inverse, un enfant n'est pas un adulte aplati.

Flux
    i Notion

    Maintenant que nous avons réglé le problème de la taille, attelons nous à celui de la chaleur. Imaginons une maison dans laquelle se trouve une poste. Des clients entrent et sortent y déposer du courrier ou en retirer.

L'entrée ou la sortie des clients constituent un flux. Le déplacement du courrier est aussi un flux. On peut mesurer l'importance de ce flux en comptant le nombre de clients en transit. Mais nombre de clients en transit et flux de sont pas la même chose. Le flux ne dépend pas de la taille de la maison, contrairement au nombre de clients. Le lien entre les deux sera donné plus loin.

    Un flux est compté à travers une surface. Cela peut être une portion de surface comme une porte, ou une surface fermée entourant un volume comme une maison. Le signe du flux indique si le volume se rempli ou se vide.

  

     ii Échange et équilibre

    Une portion de surface délimite deux régions entre lesquelles le flux transporte des éléments d'une région vers l'autre. Il y a échange entre ces régions.

 

    Cet échange peut aussi se faire entre deux surface fermées. Si le flux de la région 1 à la région 2 est égal au flux de 2 vers 1, ou si le flux entrant est égal au flux sortant, alors le flux global est nul et il y a équilibre.

    Au royaume Uni, les rues sont faites de maisons toutes identiques les unes aux autres (la rue est construite d'un bloc, rangée de briques après rangée sur toute la longueur). On peut parfois passer de l'une à l'autre par une porte latérale. Si on veut connaître le flux de personnes entre les maisons et la rue, il suffit de compter les personnes passant par les portes d'entrées seules et de ramener ce débit à la surface traversée. Le flux latéral devient invisible. A l'inverse, si on sépare une maison par une paroi, on peut faire apparaître le flux à l'intérieur. Cela est vrai même hors équilibre.

    iii Lien avec l'échelle

    Dans une maison isolée, il peut y avoir un flux de personnes à travers les murs ayant une ouverture. Si deux maisons sont accolées et que le mur commun a une ouverture, il peut y avoir un flux à travers cette cloison. Mais il n'est pas visible de l'extérieur. Cette cloison ne compte alors plus dans le calcul du débit avec l'extérieur. Si on poursuit à l'échelle d'une rue, c'est autant de surfaces qui disparaissent du bilan. Pour calculer ce bilan, il suffit d'ajouter le débit de chaque maison avec l'extérieur. Il est clair que le débit de maisons jumelles est doublé sur la façade comparé à une maison isolée. Mais le flux de chaque maison reste identique; voilà le lien entre le débit et le flux : le flux est le débit par unité de surface (intensive, extensive, voir plus bas). Si le flux est le même à travers les murs de chaque maison, alors pour avoir le nombre de personnes en transit avec la rue, il suffit d'ajouter toutes les surfaces extérieures.
    On peut aussi ajouter des étages à cette maison. Il y a alors un flux à travers le plancher, mais comme c'est un flux interne, il ne rentre pas en compte dans le bilan. Seul le flux par les façades compte. De même si les maisons de la rue ont plusieurs étages.
    Finalement, un immeuble est un bloc d'habitations qui communiquent entre elles. Bien sûr, il n'est plus question d'envisager le flux de personnes à travers les murs extérieurs, mais on peut le faire pour le bruit par exemple, ou la chaleur.

    Ces différents exemples montrent comment le débit dépend de la surface extérieure : il est la somme des flux sur toute la surface. Or la surface dépend du carré de l'échelle. Si le flux est le même pour chaque habitation, alors le débit de l'immeuble sera proportionnel au carré de l'échelle.

    Le problème traite du transfert de chaleur vis-à-vis de la taille. Il faut préciser quelques notions liées à la chaleur. La température est une mesure de l'état calorique d'un objet. Elle est indépendante de la taille de l'objet : deux casseroles d'eau chaude à la même température ne rendent pas l'eau plus chaude. Comme elle ne dépend pas du volume, on dit que c'est une grandeur intensive. À l'inverse, la quantité de chaleur emmagasinée par un objet dépend de sa taille : deux casseroles d'eau demandent deux fois plus d'énergie (gaz, électricité, ...) pour chauffer à la même température qu'une seule. La quantité de chaleur, ou énergie calorique, est une grandeur extensive. Pour fixer les idées, on peut prendre une analogie avec un réservoir d'eau; le niveau d'eau est la température tandis que le volume d'eau est l'énergie calorique. En assemblant des réservoirs, on augmente la quantité d'eau mais pas le niveau.

    Revenons à nos casseroles. Pour les chauffer, on a fait passer du courant dans une résistance électrique, ce qui a créé de la chaleur. Une résistance est une source de chaleur. Il existe des résistances qu'on peut plonger directement dans l'eau. Notre casserole se trouve alors munie de sa source de chaleur (on appelle cela une bouilloire électrique). Si on groupe plusieurs bouilloires ensemble, elles vont pouvoir chauffer plus d'eau dans le même las de temps : la quantité de chaleur créée est une grandeur extensive, mais la source n'en est pas (elle est au volume ce que le flux est à la surface).
On pourrait, par analogie, munir notre réservoir d'eau d'un petit nuage pluvieux; la pluie augmente le niveau et le volume d'eau dans le réservoir.

    Notre objet maintenant doté d'une température et d'énergie calorique va échanger de la chaleur avec son environnement, à travers sa surface. Ce flux calorique est celui qui nous intéresse ici. Comme tout flux, il est indépendant de la surface mais est lié au débit par la surface.

    Si le réservoir est muni d'un robinet, le débit d'eau dépendra du nombre de réservoirs.

    i Effet du facteur d'échelle : rapport v/s
(§ suivant très mal dit: faire une liste )

    Résumons les choses. La température dépend de la quantité de chaleur présente dans l'objet, elle-même proportionnelle au volume et dépendante de la quantité de chaleur créée par la source calorique. Cette source dépend aussi du volume, contrairement au flux qui est proportionnel à la surface. Ainsi, si Q_c est l'énergie calorique créée et Q_t celle transmise :

    Quel effet a l'échelle ? L'échelle influe sur ses quantités via le volume et la surface. Rappelez-vous, elles varient comme

    Ainsi le rapport entre ces quantités, proportionnel à v/s, varie comme l'échelle car :

    Cela signifie que quand seule la taille augmente, alors la quantité de chaleur produite augmente plus vite que la quantité évacuée.

    Avant de conclure, il nous reste encore à comprendre succinctement comment fonctionne le corps vis-à-vis de la chaleur.
La température du corps est régulée à 37.2°C normalement. Pour cela, différents moyens sont mis en œuvre comme la régulation de la circulation sanguine près de la peau ou la transpiration qui met en jeu l'absorption calorique très efficace de l'évaporation de l'eau.

    La chaleur est créée dans tout le corps par le fonctionnement normal des cellules qui brûlent des sucres pour vivre. Lors d'activité physique, les muscles travaillent plus et créent alors plus de chaleur. Faisons l'hypothèse que la masse musculaire est proportionnellement la même quelle que soit la taille (elle est liée au volume) et que l'effort est identique. Cela permet de supposer que la source de chaleur est constante et indépendante de la taille, donc que la chaleur créée est proportionnelle au volume.

    La conclusion est évidente : un adulte produit plus de chaleur qu'il ne peut en évacuer, comparé à un enfant. Or s'il garde cette chaleur excédentaire, sa température va augmenter. C'est pourquoi le corps se protège en augmentant le flux de chaleur en transpirant : l'eau emmagasine beaucoup de chaleur et en absorbe encore plus pour s'évaporer. En s'évaporant, l'eau prend cette chaleur au corps, en refroidissant la peau, et l'emmène au loin.

Autres applications

    On vient de voir qu'un enfant perd de la chaleur plus vite qu'il n'en produit, comparé à un adulte. C'est pourquoi un enfant se refroidit plus vite.

    A l'inverse, une grande taille réduit les échanges thermiques. Cela permet alors de conserver plus facilement une température constante. Aussi bien aux pôles qu'à l'équateur : un ours polaire a une taille qui lui permet de ne pas se refroidir trop vite tandis qu'un éléphant réduit ainsi le risque de surchauffe. À noter que tous deux ont une forme trapue qui se rapproche plus de la sphère. C'est normal car la sphère a le meilleur rapport v/s en ce qui concerne l'isolation. On peut s'en rendre compte facilement avec la figure suivante où le volume reste constant mais la surface augmente de gauche à droite.

1^er septembre 2002

Mise à jour : 10 octobre 2005