version française   versión Española

Introduction

    In the following, I will use the link between size and heat quantity exchanged by an object to explain some phenomenons you may have observed such as why a child is getting cold faster than an adult. The "thread" will be to answer the question: why a child does not sweat while doing an physical effort, in contrast to an adult (this, under some constraints to be explained later (same heat quantity products by the effort <> same physical effort (identical speed) for mass ~ h³)).
    To better understand the notions explained in the following, nothing is better than experimentation. So I strongly recommand you to get some chil games such as wood cubes or building bricks made of plastic before to read this document.

    Let's start with the influence of the scale on an object. In this aim, we could use a sphere (like in another document), however to help to understand, I am going to use some kind of building block

    Let's take a block to be used as a standard. We would like, for example, to obtain a block whose size is "twice" the original, in the sense that all its edges are twice longer.

    If its edges length are a, b and c, so the new block would have its edges 2a, 2b and 2c large. By extension, every distance between any two points would be twice as large; a point situated at the center of the vertical edge is at c/2 (respectivelyt c) from the nearest summits.
    With the help of the Pythagoras' theorem, it is not difficult to see that. For example, the distance between the farest two summits (They are situated on the diagonal) is, (a²+b²+c²)^1/2 for the standard block and becomes (4a²+4b²+4c²)^1/2 in the other case. In consequence, there is indeed a factor two between these distances.
    This factor is the number of time we need to carry forward the block to obtain the wished size.

    ii Surface

    Let's proceed on the same way to obtain the factor that links the large block's surfaces to the standard block. Let's filled each side and let's count the number of sides we have used .

    We can notice each side has surface four times larger than the initial side. It is normal since the surface of a rectangle is the product of two lengths; if these are enlarged with the same factor, then the surface increase with the square of this factor.

    iii Volume

    If you have understood the process until now, then you certainly have already found the solution in the case of the volume.

    The large block is formed of eight standard blocks, from where the volume is:

    iv Generalisation: scale factor

    This reasoning is not peculiar only to a two time increase of the sizes; it is also valid with a three, four, etc. time enlargement. That works as well with a reducing or for non integer factors. If h is this scale factor, then in general we get:

So, if two objects are different by their size but not their shape, then their dimensions would be like theses proportions.
A child and an adult are such two objetcs. Their sizes are different, but their shapes, to some tiny rough estimates, are identical; an adult is not the stretched version of a child and in the opposite, a child is not a flattened adult.

Flux
    i Notion

    As we now have solved the problem of the size, let's work on the heat one. We assume an house hold a post office. Customers go in and out to sent or collect mail. The moves in or out of customers form a flux. The mail move is also a flux. We can measure the importance of this flow by counting the number of customers moving through the door. But number of moving customers and flow are not the same thing; the flow doesn't depend of the house size, in contrary of the customers number. The link between both will be explain later on.

    A flux is counted through a surface. That could be a piece of a surface as a door, or a close surface surrounding a volume such as an house. The sign of the flow shows if the volume is filling up or emptying.

  

     ii Exchange and equilibrium

   A piece of a surface define two regions between which the flux carries elements from one region to the other. There is an exchange between thoses regions.

 

   This exchange can yet be done between two close surfaces. If the flux from the region 1 to the region 2 is equal to the flux from 2 to 1, or if the flux in is equal to the flux out, then the total flux is nil and there is equilibrium.
    In UK, streets are made of houses identical to each other (the street is built in once, rows of bricks after rows all along the street ;o) ). Sometime it is possible to walk from one to the other through a common door. If we want to know, the flux of persons between the houses and the street, it is enough to count only the people walking through the main doors and to compare this output with the crossed surface. The common wall flux becomes invisible. On the opposite, if we separate an house with a wall, the inside flux can appear. This is true even when the equilibrium is not reached.

    iii Link with the scale

    In an standing alone house, a flux of persons through walls with an opening can happen. If two such houses are adjacent and share an opening in the common wall, a flux can cross this wall. However it is now invisible from the outside. This wall doesn't count any more in the calculation of the output with the outside. If we do so on the scale of a street, it is so many walls that disappear of the balance. To sum up this, we only need to add the output of each house with the outside. It is clear that the output of twin houses is doubled on the front compare with an house standing alone. But the flux of each house stays the same; here is the link between output and flux: the flux is the output per unit of surface (intensive, extensive). If the flux is the same through all the walls of each house, then to know the number of persons in transit with the street, we only need to add all the outside surfaces.
   Also we can add stairs to this house. Then there is a flux through the floors, but as it is an inside flux, it is not used in the balance. Only the flux through the sides is useful. It is the same if the street houses have stairs.
    Finaly, a building is a block of flats that pass on to each others. Of course, we are not going to consider the flux of persons through the outside walls, but we can do this with sound, for example, or heat.
    Thoses different examples show how the output depends of the outside surface: it is the sum of the flux over the whole surface. Now, surface depends of the square of the scale. If the flux is the same for all flats, then the building output will be in the same proportion as the scale to the square.

    The problem deal with the heat transfert versus the size. We have to clarify some notions related to heat. Temperature is a measurement of the heat state of an object. It is independant of the object size: two pans filled with hot water at the same temperature don't make the water warmer. As it is not dependant of the volume, it is said to be intensive. On the contrary, the heat quantity stored by an object depends of its size: two water pans need twice the energy (gas, electricity, ...) to heat at the same temperature than an only one. The amount of heat, or heat energy, is an extensive quantity. In order to well understand, we can draw an analogy with a water tank; the water level is the temperature while the water volume is the heat energy. Gathering tanks together, increases the amount of water but not its level.

    Let's back to our pans. To heat them up, current circulates in a resistor, which produces heat. A resistor is a heat source. There is resistors able to work in water. Our pan is then fitted with its own heat source (this is usualy called an electric kettle). If we gather several kettles, they are able to heat more water in the same time: the amount of heat produced is an extensive quantity, but the source is not one (it is in the same relation with the volume that the flow is with the surface).
Drawing an analogy, we could fit our water tank with a little rainy cloud; rain increase the water level and volume in the tank.
    Our object, now fitted with a temperature and a heat energy, is going to exchange heat with its vicinity, through its surface. This heat flow is whose we are interested in here. As every flow, it is independant of the surface area but is linked to the rate of flow through the surface.

    If the tank is fitted with a tap, the rate of flow depends of the number of tanks.

    i Effect of the scale factor: ratio v/s
(§ suivant très mal dit: faire une liste )

    Let's sum up all this. Temperature depends of the heat amount contained in the object, which is proportional to the volume and depends of the amount of heat produced by the heat source. That source also depends of the volume, in opposite to the flow which is proportional to the surface. So, if Q_c is the heat energy produced and Q_f the one transmitted:

    What effect does the scale have ? The scale has an influence on those quantities through the volume and the surface area. Remember, they change like

    So the ratio between those quantities, proportional to v/s, change with the scale for:

    This means that when only the size increases, then the amount of heat produced increases faster than the amount lost.

    Before we conclude, we still have to quickly understand how works the body in relation to heat.
Body temperature is usually regulated at 37.2°C. To achieve this, several means are used such as skin blood circulation control or sweating which uses the very efficient heat absorption of water evaporation.
    Heat is produced in the whole body by usual cells functioning, which burn 'sugar' to live. During physical activities, muscles work more and then produce more heat. We make the assumption that muscle mass is always in the same proportion to the size (ie is related to the volume) and that physical activity is the same. This allows us to assume the heat source is a constant and independant of the size, and so that the produced heat is proportional to the volume.
    The conclusion is an evidence: an adult produces more heat than he can lost, compared to a child. And yet if he keeps this excess of heat, his temperature is going to increase. This is why the body is protecting itself by increasing the heat flow with sweating: water stores a lot of heat and absorbs even more to evaporate. While evaporating, water takes that heat away from the body, and cools the skin down.

Other applications

    We have just seen a child losts heat faster than he produces it, compared to an adult. This is why a child cool down faster.
    In the contrary, a large size reduces heat transferts. Then this allows to keep a constant temperature more easily. This is true at the poles as well as on the Equator: a polar bear has a size allowing him not to cool down too quickly while an elephant reduces this way the risk to overheat. It is to notice that both have a thickset shape that is close to a sphere. 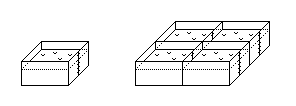This is normal for a sphere has the best v/s ratio according to insulation. It is easy to notice this with the following figure where the volume remains constant while the surface increases from left to right.

1^st September 2002