English version   version française

Introducción

   En lo que sige, voy a utilizar la relación que existe entre la tamaño y la cuantía de calor cambiada por un objecto para explicar fenomenones que pudo observar como el hecho que un niño se refresca más rapido que un adulto. El hilo será de responder a la pregunta : ¿ por qué un niño no suda, haciendo un esfuerzo físico, al contrario de un adulto (este, con algunas obligaciones que se evocarán más luego (la misma cuantía de calor producida por el esfuerzo <> el mismo esfuerzo fisíco (velocidad identica) por que mass ~h³)) ?
   Para comprender mejor las nociones explicadas en lo que segui, nada vale la experimentación. Pues le aconsejo de pronto de procurarle jugos para los niños como cubos o ladrillos de construcción de plástico antes de semir en este codumento. Pour mieux comprendre les notions expliquées dans la suite, rien ne vaut l'expérimentation. Je vous conseille donc vivement de vous procurer des jeux pour enfants tels que des cubes ou des briques de construction en plastique avant de plonger dans ce document.

   Empezamos a ver cual es la influenza de la tamaño sobre un objecto. Por eso podria mos tomar una esfera (como en un otro documento), pero para ayudar a comprender, voy a escoger un adoquín rectangular. Commençons par voir quel est l'influence de la taille sur un objet. Pour cela nous pourrions prendre une sphère (comme dans un autre document), mais pour aider à la compréhension, je vais choisir un pavé rectangulaire

   Consideramos un adoquín, que servirá de patrón. Se quiere, por ejemplo, obtener un adoquín "dos veces más alto", con el sentido que todas sus aristas sean dos veces más largas.

   Si sus aristas hacen a,b y c de extensión, entonces el nuevo adoquín tenera aristas de extensión 2a, 2b y 2c. En general, toda distancia entre dos cualquieres puntos será dos veces más larga; un punto localizado en el centro de la arista vertical es a c/2 (respectivamente c) de los más cercanos vértices.
   Con la ayuda de la relación de * Pythagore*, no es difícil de advertirselo. Por ejemplo, la distancia entre dos vértices los más alejados (son localizados sobre la diagonal) es, (a²+b²+c²)^1/2 para el adoquín patrón y se vuelve (4a²+4b²+4c²)^1/2 en el segundo caso. Ya hay un factor dos entre estas distancias.
   Este factor es el número de veces necesario para transportar el adoquín a fin de obtener la extensión deseada.

    ii Surperficie

   Procedemos de la misma manera para obtener el factor que liga las superficies del gran adoquín al adoquín patrón; llenamos cada frente y calculamos el número de frentes utilizadas.

   Se observa que cada frente tiene para área, el cuádruplo de la frente iniciala. Es normal pues la superficie de un rectángulo es el producto de dos distancias; si éstas estan agrandidas del mismo factor, entonces la superficie aumenta del cuadrudo de este factor.

    iii Volumen

   Si ha comprendido el proceso hasta aquí, entonces ya ha ciertamente descubierto la solución para el volumen.

   Al adoquín grande es formado de ocho adoquines patrones, por donde el volumen es :

    iv Generalización : factor de escala

   Este razonamiento no está más proprio que a una duplicación de las dimensiones; está también valedero para un ensanche triple, cuádruple, etc. Esa anda también con una reducción o con factores que no son enteros. Si h está este factor de escala, entonces se tiene en general :

Así, si dos objectos diferen por el tamaño pero no por la forma, entonces sus cuantías espaciales serán de estas proporciones.
Un niño y un adulto son dos tal objectos. Sus tamaños diferen, pero sus formas, aproximadamente, son idénticas; un adulto no es la versión estirada de un niño y al contrario un niño no es un adulto aplastido.

Flujo
    i Noción

    Ahora que hemos resuelto el problemo del tamaño, nos consagremos al de la calor. Imaginemos una casa en la que se encuentra un correo. Clientes entran y salen ahí dejar o sacar correo. La entrada o la salida de los clientes constituen un flujo. El traslado del correo está tambien un flujo. Se puede mesurar la importancia de este flujo contando el número de clientes en tránsito. Pero número de clientes en tránsito y flujo no son exacto la misma cosa. El flujo no depende del tamaño de la casa, al contrario del número de clientes. La relación entre los dos es dada luego.

    Un flujo está contado a través de una superficie. Ésta puede ser una porción de superficie (aréa) como una puerta, o una superficie cerrada cercando un volumen como una casa. Su signo indica si el volumen se rellena o se vacia.

  

     ii Cambio y equilibrio

    Una aréa delimita dos regiones entre las cuales el flujo traslada elementos de una región a la otra. Hay cambio entre sus regiones.

 

    Este cambio puede también hacerse entre dos superficies cerradas. Si el flujo de la región 1 a la región 2 está igual al flujo de 2 a 1, 0 si el flujo entrando está igual al flujo saliendo, entonces el flujo global está nulo y hay equilibrio.
    En el Reino Unido, calles están hechas con casas todas identicas las unas a las otras (la calle está construida en una vez, hilera de ladrillos antes hilera sobre toda la longitud). A veces, se puede pasar de una casa a la otra por una puerta lateral. Si se quiere conocer el flujo de personas entre las casas, y la calle, basta con contar las personas pasando por las puertas de entrada solas y de dividir este caudal con la superficie atraversada. El flujo lateral deviene invisible. Al contrario, si se separa una casa con una pared, se puede hacer aparecer el flujo en el interior. Este está verdad incluso fuera del equilibrio.

    iii Vínculo con la escala

    En una casa aislada, se puede haber un flujo de personas a través las paredes con una abertura. Si dos casas son appareilladas y que la pared común tiene una abertura, se puede haber un fluro a través este tabique. Pero, no está visible del exterior. Pues este tabique ya no cuenta en el cálculo del caudal con el exterior. Si se prosigue al escala de una calle, es tanto superfies que desaparecen del total. Para calcular éste, es suficiente de añadir el caudal de cada casa con el exterior. 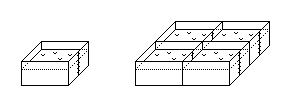Es claro que que el caudal de casas gemelas está doblado en la fachada comparado a una casa aislada. Pero el flujo de cada casa queda el mismo; ahí está el vínculo entre el caudal y el flujo : el flujo es el caudal a través una unidad de área (intensiva, extensiva). Si el flujo está el mismo a través las paredes de cada casa, entoncés para conocer el número de personas en tránsito desde la calle, es suficiente de añadir todas las áreas exteriores.
    Se puede tambien añadir pisos a esta casa. Entoncés hay un flujo a través el suelo, pero como es un flujo interno, no le tienen en cuento en el *total*. Solo el flujo por las fachadas cuenta. Asimismo, si las casas de la calle tienen varios pisos.
    Al fin, un edificio está un grupo de pisos comunicandos entre ellos. Por supuesto, ya no se trata de enfocar el flujo de personas a través las paredes exteriores, pero se puede hacerlo con el ruido por ejemplo, o el calor.
    Estos varios ejemplos muestran como el caudal depende de la superficie exterior : es la suma de los flujos sobre toda la *area*. Ahora bien la *area* depende del cuadrado de la escala. Si el flujo está el mismo para cado piso, entoncés el caudal del edificio estará proporcional al cuadrado de la escala.

    El problemo trata del traslado de la calor con respecto al tamaño. Hay que precisar algunas nociones relativas a la calor. La temperatura es una medida del estatuto calórico de un objecto. Es independiente del tamaño del objecto : dos cazos de agua caliente con la misma temperatura no vuelven el agua más caliente. Como no depende del volumen, se dice que es una cantidad intensiva. Al contrario, la candidad de calor accumulada por un objecto depende de su tamaño : dos cazos de agua necesiten dos veces más de energía (gas, electricidad, ...) para calentar a la misma temperatura que una. La cantidad de calor, o de energía calórica, es extensiva. Para asentar las ideas, se puede hacer una analogía con un depósito de agua; el nivel de agua está la temperatura mientras que el volumen de aqua está la energía calórica. Juntando depósitos, se incrementa la cantidad de agua pero no el nivel.

    Volvemos a nuestros cazos. Para calentarlos, se hacen pasar corriente en una resistancia eléctrica, lo que produce calor. Una resistancia está una fuente de calor. Hay resistancias que se puede sumergir en el agua. Entoncés nuestro cazo està proveido con su fuente de calor (se llama un hervidor eléctrico). Si se agrupa unos hervidos juntos, van a poder calentar más agua en el mismo tiempo : la cantidad de calor creada es una cantidad extensiva, pero la fuente no es una (es para el volumen como el flujo es para la superficie).
Se puede, por analogía, proveer nuestro depósito de agua con una nubecita lluviosa; la lluvia incrementa el nivel y el volumen de agua en el depósito.
    Nuestro objecto ahora dotado de una temperatura y de energía calórica va a cambiar calor con su medio ambiente, a través su superficie. Este flujo calórico está el que nos importa aquí. Como cualquier flujo, es independiente de la superficie pero es vínculado al caudal por la superficie.

    Si el depósito está proveido con un grifo, el caudal de agua dependerá del número de depósitos.

    i Effecto del factor de escala : razón v/s
(§ suivant très mal dit: faire une liste )

    Resumamos lo dicho anteriormente. La temperatura depende de la cantidad de calor presente en el objecto, la que está proportional al volumen y depende de la cantidad de calor creada por la fuente calórica. Ésta depende tambien del volumen, al contrario del flujo que está proportional a la surperficie. Así, si Q_c está la energía calórica creada y Q_f la transmitida :

    ¿ Que effecto tiene la escala ? La escala influe sobre estas cantidades por el volumen y la superficie. Recordad, varian como

    Así la razón entre estas cantidades, proportional a v/s, varia como la escala porque :

    Eso significa que cuando solo el tamaño aumenta, entoncés la cantidad de calor producida aumenta más rápidamente que la cantidad evacuada.

    Antes de concluir, nos quedamos todavía a comprender sucintamente como funciona el cuerpo en frente de la calor.
La temperatura del cuerpo está regulada a 37,2°C normalmente. Por eso, varios medios son empleados como la regulación de la circulación de la sangre cerca de la piel o el sudor que pone en juego la absorción de calor muy eficaz de la evaporación del agua.
    La calor es creada en todo el cuerpo por el funcionamiento normal de las células que consumen azucares para vivir. Durante una actividad física, los músculos travajan más y entoncés crean más calor. Hagamos la hipótesis que la masa muscular está proporcionalmente la misma cualquiera que sea el tamaño (es vinculada al volumen) y el esfuerzo está idéntico. Eso permiti de suponer que la fuente de calor está constante y independiente del tamaño, pues que la calor creada está proporcional al volumen.
    La conclusión está evidente : un adulto produce más calor que puede evacuar, comparado a un niño. Ahora si conserva esta sobrante calor, su temperatura va a aumentar. Así para ampararse, el cuerpo aumenta el flujo de calor sudando : el agua acumula mucha calor y absorba todavía más para evaporarse. Al evaporar, el agua saca esta calor al cuerpo, enfriando la piel, y la lleva a lo lejos.

Otras aplicaciones

    Vamos a ver que un niño pierde calor más rapidamente que la produce, comparado a un adulto. Es porque un niño se enfria más rapidamente.
    Al contrario, un gran tamaño reduce los cambios termicos. Pues eso permite de conservar más fácilmente una temperatura constante. Tanto a los polos como al equador : un oso polar tiene un tamaño que le permite de no refriarse demasiado de prisa mientras que un elefante reduce así el riesgo de recalentamiento. Observad que los dos tienen una forma rechoncha que se acerca de la esfera. Es normal porque la esfera tiene la mejor razón v/s en lo que concierne la aislamiento. Podemos darse cuenta de eso fácilmente sobre la figura siguiente donde el volumen queda constante pero la superficie aumenta de la izquierda a la derecha.

1 Septiembre 2002