 English version
English version  versión Española
versión Española
 English version
English version  versión Española
versión Española
Commençons par le commencement. Nous avons tous fait cette expérience d'enrouler une ficelle autour d'un axe et de tirer. Et nous avons tous fait les mêmes constatations : ça résiste, mais ça ne tient pas. Et on se retrouve avec la ficelle dans une main, l'axe dans l'autre.
On tombe déjà sur ce constat : si jamais Indy s'est pendu à son fouet, notre aventurier est par terre ! Vous me direz, c'est une histoire, pourquoi couper les ficelles en quatre ? Et bien si la ficelle ne tient pas, on a quand même senti une résistance. Il y a donc un espoir, une possibilité qu'Indy passe de l'autre côté ou tout au moins qu'il tienne jusque là.



Que se passe-t-il donc quand on enroule la ficelle pour qu'on sente une résistance ? La réponse est très simple. Il y a frottement (solide) entre la corde et son support (l'axe). Le plus simple pour s'en rendre compte est de faire l'expérience suivante ; passer une corde à cheval sur un support , de préférence rugueux et large, y attacher à hauteur égale des masses égales. Le tout est en équilibre ce qui est normal puisque le support joue ici le rôle d'une poulie. Si on ajoute à l'un des poids un peu de poids, à un moment l'équilibre sera rompu et la corde et les poids glisseront. Mais dans cet intervalle de poids, l'équilibre est maintenu malgré la différence de poids. Cela est due au frottement de la corde sur le support. Avec une poulie ce frottement serait inexistant et la corde basculerait.

On peut d'ailleurs utiliser cette expérience pour mesurer le coefficient de frottement de la corde sur son support.

Le frottement le long du demi cylindre supérieur compense la différence de poids limite, soit,
δPmax = π.r.µ
où µ est le coefficient de frottement moyen sur un demi tour. Il dépend naturellement de la nature du support et de la corde, la corde glissera plus facilement sur une barre d'acier que sur une branche ou si elle est en nylon plutôt qu'en chanvre. La pression ou la tension aussi joue un rôle. Sur une surface plane de même nature que l'axe (support), la corde glissera moins si on appuie dessus. Sur une surface incurvée la tension de la corde a le même effet car elle va avoir tendance à tirer la corde vers l'axe du support, donc à la presser contre.

Donc une corde soutenant deux poids importants glissera sous un excès de poids plus important qu'une corde libre de poids.


Maintenant qu'on comprend mieux l'origine de cette résistance, on y voit plus clair sur les moyens de la mettre en œuvre pour faire traverser notre intrépide archéologue (héros). Approfondissons tout d'abord ce frottement.

Comment pourrions-nous optimiser ce frottement ? Si vous avez bien lu ce qui précède, vous avez déjà en tête les deux moyens. Il s'agit soit d'augmenter la coefficient de friction, soit que les frottements aient lieu sur plus de corde. Comme il est hors de question de changer son support, on peut oublier tout ce qui s'y rapporte (taille, nature, ...). On peut par contre agir sur la nature de la corde et la longueur de corde travaillant.
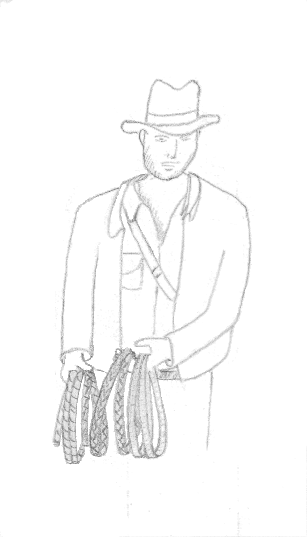

Prenons des fouets de nature différente : une corde, du caoutchouc et une lanière ou une sangle. La corde nous servira de témoin pour comparer.
Chacun sait que le caoutchouc adhère mieux que la corde ou le cuir. Cela signifie qu'il a un coefficient de frottement plus élevé que celui de la corde. Selon la formule trouvée plus haut, cela signifie que la différence de poids entre les deux brins que peut compenser la corde par les frottements sera plus élevée avec du caoutchouc qu'avec une corde normale.
Un autre moyen d'augmenter l'adhérence est d'augmenter la surface en contact ; c'est très simple à comprendre, en imaginant qu'Indy n'utilise pas un mais deux fouets en parallèle : la surface en contact avec le support sera doublée et notre différence de poids supportée sera double. Cela reviendrait à avoir un coefficient de frottement double, 2µ. Il est plus correct d'ajouter un facteur Φ qui tient compte de la largeur de la corde en contact (diamètre pour une corde cylindrique, largeur pour une sangle).
δPM = µ.r.Φ.π
L'exemple précédent de deux cordes côte à côte suggère une autre optimisation. Au lieu de prendre plusieurs cordes ou une corde de diamètre supérieur, pourquoi ne pas utiliser la même corde et la faire à nouveau passer au dessus du support une, deux ou plusieurs fois ! En tenant toutes les boucles à la fois, on aura l'équivalent.
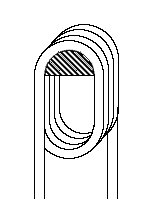

δPM = µ.r.n.Φ.π
Évidemment, ça n'est guère pratique et une meilleure solution existe. Elle est évidente : enrouler la corde sur le support afin qu'elle soit au maximum en contact à chaque tour, et exercer les forces sur les extrémités. On ne peut malheureusement plus utiliser la formule moyenne précédente car la force qui s'exerce sur chaque portion de corde n'est plus la même (précédemment, on tenait tous les tours à la fois, ce qui répartissait le poids sur chaque tour) ; or le coefficient de frottement dépend de la pression, donc de la tension sur le brin. De même, l'expression précédente est peu utile car elle fait intervenir un frottement moyen qui dépend du coefficient de frottement réel et de la pression.
On peut cependant faire une estimation grossière en définissant un frottement moyen différent à chaque tour. La différence de poids est la somme des différences de tensions aux extrémités de chaque tour qui dépendent du frottement moyen de chaque tour. Si n est le nombre complet de tours, sur un support cylindrique, on a avec le demi tour supplémentaire
δPM = Σ δTi = µ1.2π.r.Φ+ ... + µn.2π.r.Φ = (Σ µi).2π.r.Φ

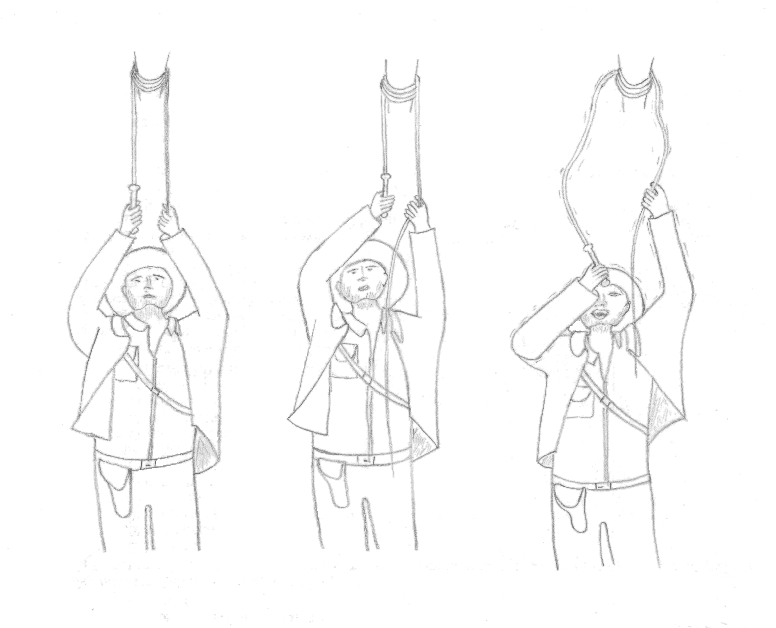
On pourrait croire qu'on a trouvé la solution, mais il n'en est rien. C'est un début de réponse qui est vrai dans un cas de figure limité. Nous avons réfléchi en comparant la différence de poids suspendus aux extrémités. Sans poids, avec une extrémité libre, on ne peut suspendre que de faibles masses, même avec de nombreux tours. La raison a été évoqué plus tôt ; les frottements augmentent avec la tension de la corde. Or s'il y a une grande différence de poids, et surtout si l'une des extrémités est libre, la tension et les frottements de ce côté seront faibles, ce qui ne permettra pas de compenser le poids de l'autre côté. En fait, la tension pour retenir le poids est proportionnelle à ce poids donc elle ne peut être nulle.
De façon plus approfondie, en ne considérant pas les frottements moyens sur un tour complet mais les frottements sur un petit élément de corde, et en supposant que le coefficient de frottement solide est proportionnel à la pression donc la tension, on montre que la tension décroît comme
e-µ.α/Φ
d'où on déduit la relation d'atténuation de la tension par tour,
T1 = ε.To
où ε = e-µ.2π/Φ
et pour un nombre de tours quelconque n,
Tn = εn.To
ce qui est valable aussi pour un nombre non entier de tours (cf. annexe 1).
En pratique, il faut au moins une masselotte (le poids de la corde ne suffit pas).
L'explication est la suivante : on a dit que les frottements étaient solides. Cela signifie qu'on peut exercer une force sans que la corde ne bouge tant qu'elle ne dépasse pas une certaine valeur. Une fois celle-ci atteinte, le mouvement a lieu. C'est ce qui permet de suspendre un poids inférieur à cette limite.
Les tours ont donc
pour but de réduire la
traction au minimum mais il faut toujours l'opposer par une force
contraire pour passer sous cette limite. La masselotte est un moyen de
l'obtenir. Il en existe un autre que nous verrons plus loin, mais avant,
Les résultats précédents nous ont montrés qu'il était possible de réduire la force à opposer à la traction pour qu'il n'y ait pas glissement et chute de notre héros. Si cette force est supérieure à
alors l'enroulement supportera jusqu'à To. Cependant, il faut d'assez nombreux tours pour avoir une atténuation convenable pour supporter le poids d'un homme ou plus, et un fouet n'a que rarement une masselotte à l'extrémité. Aussi ce résultat n'est pas celui qui permettra à Indiana Jones de se suspendre durablement avec son fouet. Tout au plus peut-il maintenant espérer rester suspendu une petite poignée de secondes.
Il faudrait trouver un moyen d'opposer une force à l'extrémité sans passer par une masselotte, en maintenant l'extrémité en place et en la retenant sans qu'elle ne glisse. Sans doute avez-vous déjà une idée : pourquoi ne pas faire un nœud ! On parvient à l'aide de nœuds à accrocher une corde à un objet pour s'y suspendre ou le tirer à soi, et cela marche.
Mais pourquoi un nœud
tient-il ? Et tient-il mieux qu'un simple enroulement avec contre poids
? Attention au mal de crâne !
Pour cela, il faut étudier le nœud le plus simple : la superposition de deux brins sur le support. Ne nous occupons pas de la façon dont les brins finissent de s'enrouler autour du support.
[image]
Le brin inférieur est toujours soumis aux mêmes forces que précédemment. Il y a en plus de nouvelles forces à l'emplacement du chevauchement :
On devine immédiatement qu'un frottement accru revient à diminuer la force d'opposition de façon différente que ce que nous avons déterminé plus haut ; on va donc avoir un "décrochage" de la tension en passant sous le brin supérieur ce qui pourrait permettre de tomber sous une tension nulle et ainsi de compenser la tension qui s'exerce juste avant cette superposition.
[image : Indy enfin satisfait]
On a vu plus haut que les frottements dépendaient de la pression exercée. S'il y a une augmentation moyenne δP de pression, alors les frottements de la corde inférieure sur le support augmenteront de
D'autre part, les frottements entre brins ajoutent une seconde force. On peut l'estimer grossièrement en supposant que le brin supérieur va s'enrouler autour du brin inférieur de la même manière que plus haut le brin s'enroulait autour du support. On obtient ainsi une force qui varie comme une exponentielle de raison le coefficient de frottement entre cordes et un frottement moyen de la forme
Ces deux forces strictement positives, peuvent donc dépasser la tension résiduelle à l'extrémité de la corde et ainsi s'opposer à ce que la corde ne glisse. En fait, la condition pour que la corde ne glisse pas devient,
où T1 est la traction sur le brin supérieur avant le chevauchement, T3 la traction sur le brin inférieur avant le chevauchement et T4 la force d'opposition [cf. annexe 2].
Voilà la solution : il suffit qu'Indy fasse un nœud du bout de son fouet ! Plus facile à dire qu'à faire.
Si on complète les brins du paragraphe suivant, on voit autre chose poindre à l'horizon. Prolongeons le brin 2 vers le brin 3 ; la tension en 3 va dépendre de la tension en 2 selon la première loi trouvée ; il y a équilibre si
T3 ≥ ε.T2
Comme cette
dernière dépend de la tension avant le chevauchement par
une loi similaire, l'équilibre existe si,
T2 ≥ ε'.T1
la tension en 3 dépend directement de la tension en 1 et la condition d'équilibre devient,
soit en combinant les trois inégalité,
ε.ε'.T1 ≤ ω.T1 + T4
ε' est proche de 1. ε est inférieur
à 1. ω pourrait être quant à lui supérieur
à 1. On voit donc qu'il y a possibilité dans certains cas
que cette condition soit réalisée sans avoir besoin
d'exercer une force d'opposition. Cela est vrai à la condition,
Mieux, cette condition resterait vraie quelle que soit l'intensité de T1 . Cela signifie qu'un tel nœud tiendrait sans glisser à toute force de traction, jusqu'à la rupture. Cela dépend donc uniquement des coefficients de frottement corde-support et corde-corde, ce sont des propriétés uniques au couple choisi.
Nous allons voir dans la section suivante quelques exemples de nœuds qui tiennent jusqu'à la rupture ou qui glissent.
Voici quelques exemples pour apprendre comment appliquer ces résultats. Nous prendrons le nœud de cabestan et ses variantes pour comprendre quelle partie du nœud est à étudier et quel nœud est le plus solide. On va aussi voir un simple enroulement avec une superposition par le brin où la traction s'exerce.
Le nœud de cabestan est formé de deux
enroulements et deux superpositions. Dans l'ordre depuis le brin sous
tension, il y a une superposition (1), l'enroulement (2) et l'autre
superposition.
On détermine alors les conditions de glissement sur chaque section. Intuitivement, la seconde superposition sera plus cruciale que la première d'abord parce que les enroulements auront atténué la tension mais que la force de superposition sera la même, et aussi parce que le brin est libre après la seconde. L'atténuation de l'enroulement à elle seule ne permet pas au nœud de ne pas glisser, comme on l'a vu dans la première partie de ce document.
Mathématiquement, cela s'exprime par le système d'inéquations suivant,
soit,
Voici un exemple de
nœud très simple qui tiendrait relativement bien, noué
à l'extrémité et qui pourrait se défaire
facilement même après avoir été sous
tension. Attention ! Il peut toutefois se dénouer sous tension,
attention si vous l'essayez. Sa simplicité, le fait d'être
noué à l'extrémité et de pouvoir
être défait depuis l'autre extrémité en fait
le candidat idéal pour notre aventurier.
On remarque que la condition de non glissement à la
superposition est essentielle pour qu'un nœud tienne. Aussi, un nœud
qui est principalement formé de superpositions est un des nœuds les plus
solides. Le nœud de bois est un tel nœud ; il consiste en une
boucle torsadée à l'extrémité de la corde dans laquelle on fait passer
le brin à nouer après l'avoir fait passer autour du support.
Une variante de ce
nœud peut être défaite en secouant la corde ; il
suffit de ne faire qu'un demi-tour à la torsade. La corde
s'enroule donc
autour du support, fait une boucle autour de la corde et le brin libre
repasse sous la corde enroulée sous le support. On a un
enroulement (1), une superposition (2) et un autre enroulement (3)
formé par la boucle autour de la corde dont on peut tenir compte
; son coefficient corde sur corde est différent.
Il n'a pas été tenu compte des
frottements entre tours voisins. D'abord, cela n'est guère utile
puisque souvent les tours s'enroulent dans le même sens et lors
d'un glissement, ils tournent en étant immobiles, l'un
relativement à l'autre. Seuls quelques cas comme le nœud
d'alouette ont des brins pouvant tourner en sens inverse. Ensuite, les
frottements seront encore de type solide, ce dont on pourrait tenir
compte en modifiant la valeur de µ. L'expression exacte finale
deviendrait un peu plus compliquée car il faudrait tenir compte
du bon coefficient pour chaque portion de tour, mais qualitativement,
on obtiendrait les mêmes résultats : atténuation
exponentielle.
En conclusion, on remarque qu'il est quasi impossible en réalité que notre héros puisse se suspendre à son fouet en ne le nouant que par un coup de fouet. À moins d'avoir un doigté extraordinaire, ce qui est normal pour un personnage de fiction, ou d'avoir beaucoup de chance, il n'est pas possible de s'y suspendre. Cependant, les conditions n'en sont pas loin ce qui laisse un côté réaliste à ce geste.
J'espère ainsi vous avoir
intéressés aux nœuds et à la physique qui leur
permet de tenir. Ainsi, j'espère que la prochaine fois que vous
ferez un nœud, vous ferez attention à faire le bon et que vous
saurez pourquoi c'est le bon.
Hypothèses

 β
: angle des forces sur la corde supérieure. Dépend de la géométrie du chevauchement
β
: angle des forces sur la corde supérieure. Dépend de la géométrie du chevauchement P' est uniforme sur toute la superposition -> P' moyen
P' est uniforme sur toute la superposition -> P' moyen