¿Indy puede cruzar con su látigo?

    En la gruta, Indiana Jones es proseguido por los sbires de Shiva. Se encuentra acuñado por un precipicio encendido. Desenvaina sdon látigo, advierte una viga y hace crujir el látigo. Éste se envuelve en torno a la viga y nuestro héroe al Fedora se vuela en los aires y se encuentra del otro lado del precipicio, sano y excepto. Una pequeña sacudida y se retira el látigo.
    En la película, se salva a Indy porque el látigo se agarra firmemente a la viga. ¿Pero en la realidad, el látigo habría tenido? Es lo que vamos a ver.

Fricciones

    Comencemos por el principio. Tenemos todo hecho esta experiencia de envolver una cuerda en torno a un eje y de extraer. Y tenemos todo hecho las mismas comprobaciones: eso resiste, pero eso no tiene. Y se se encuentra con la cuerda en una mano, el eje en otro.

    Ya se cae sobre esta acta: ¡si Indy se colgó a su látigo, nuestro aventurero es de tierra! ¿Me dirán, la esta historia, por qué que corte las cuerdas en cuatro? Y bien si la cuerda no tiene, a pesar de todo se sintió una resistencia. Hay pues una esperanza, una posibilidad que Indy pasa del otro lado o por lo menos que tenga hasta allí.

    ¿Qué pasa pues cuándo él envuelve la cuerda para que se sienta una resistencia? La respuesta es muy simple. Hay fricción (sólido) injerto la cuerda y su apoyo (el eje). El más simple para darse cuenta es hacer la experiencia siguiente; pasar una cuerda a caballo de un apoyo, preferiblemente rugeux y amplio, allí ligar a altura igual de las masas iguales. ¿Todo ello está en equilibrio lo que es normal puesto que el apoyo desempeña aquí el papel de una polea? Si se añaden al uno de los pesos un poco de pesos, en un momento el équlibre se romperá y lo tuerce y los pesos deslizarán. Pero en este intervalo de peso, el equilibrio se mantiene a pesar de la diferencia de peso. Eso se debe a la fricción de la cuerda en el soporte. Con una polea esta fricción sería inexistente y la cuerda oscilaría.

    Se puede por otra parte utilizar esta experiencia para medir el coeficiente de fricción de la cuerda en su soporte.

    La fricción a lo largo de la mitad rueda a superior compensa la diferencia de peso límite, o sea,

δP_max = π.r.µ

dónde µ es el coeficiente de fricción. Depende naturalmente de la naturaleza del apoyo y la cuerda, la cuerda deslizará más fácilmente sobre una barra de acero que sobre una rama o si es de nilón más bien que en cáñamo. La presión o la tensión también desempeña un papel. Sobre una su plana de la misma naturaleza que el eje (apoyo), la cuerda deslizará menos si él ap parte. Sobre una superficie curvada la tensión de la cuerda tiene el mismo efecto ya que va a tender a extraer la cuerda hacia el eje del apoyo, por lo tanto a presionarla contra.

    Pues una cuerda que apoyará dos pesos importantes deslizará bajo un exceso de peso más importante que una cuerda libre de peso).

    Ahora que se comprende mejor el origen de esta resistencia, se se ve más claramente sobre los medios de ponerla en œ para hacer cruzar a nuestro héroe. Profundicemos en en primer lugar esta fricción.

    ¿Cómo podrían optimizar esta fricción? Si leyeron bien lo que precede, ya tienen en cabeza los dos medios. Se trata sea aumentar el coeficiente de fricción, bien que las fricciones tengan lugar sobre más cuerda. Como es inaceptable cambiar su apoyo, se puede olvidar todo lo que se produce beneficio (tamaño, naturaleza...). él puede por el contrario actuar sobre la naturaleza de la cuerda y la longitud de cuerda que trabaja.

      

Máximos aprovechamientos

    Tomemos látigos de diferente carácter: una cuerda, del caucho y una correa o una correa. La cuerda nos servirá de testigo para comparar.

    Cada uno sabe que el caucho se adhiere mejor que la cuerda o el cuero. Eso significa que tiene un coeficiente de fricción más elevado que el de la cuerda. Según la fórmula encontrada más arriba, eso significa que la diferencia de peso entre los dos pocos que puede compensar la cuerda por las fricciones será más elevada con caucho que con normal.

    Otro medio de aumentar la adherencia es aumentar del syrface en contacto; es muy simple de incluir, imaginándose que Indy no utiliza uno pero dos látigos eb paralelo: se duplicará la superficie en contacto con el apoyo y nuestra diferencia de peso soportada será doble. Eso equivaldría a tener un coeficiente de fricción doble, 2µ. Es más correcto añadir un factur que tiene en cuenta la longitud de la cuerda en contacto (diámetro para una cuerda cilíndrica, anchura para una correa).

δP_M = µ.r.d.π

    El ejemplo anterior de dos cuerdas costa a costa sugiere otro máximo aprovechamiento. ¡En vez de tomar varias cuerdas o una cuerda de diámetro superior, porqué no utilizar la misma cuerda y hacerlo de nuevo pasar sobre el apoyo uno, dos o varias veces! Al tener todos los cierres a la vez, se tendrá el equivalente.

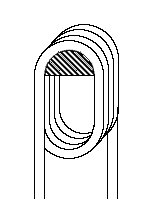
δP_M = µ.r.n.d.π

    Obviamente, eso es práctico apenas y una mejor solución existe. Es evidente: envolver la cuerda en el soporte para que sea al máximo en contacto  a cada vuelta, y ejercer las fuerzas sobre las extremidades. Si n es el número completo de vueltas, en un soporte cilíndrico, se tiene con la mitad vuelta suplementaria

δP_M = µ.2π.r.(n+1/2).d

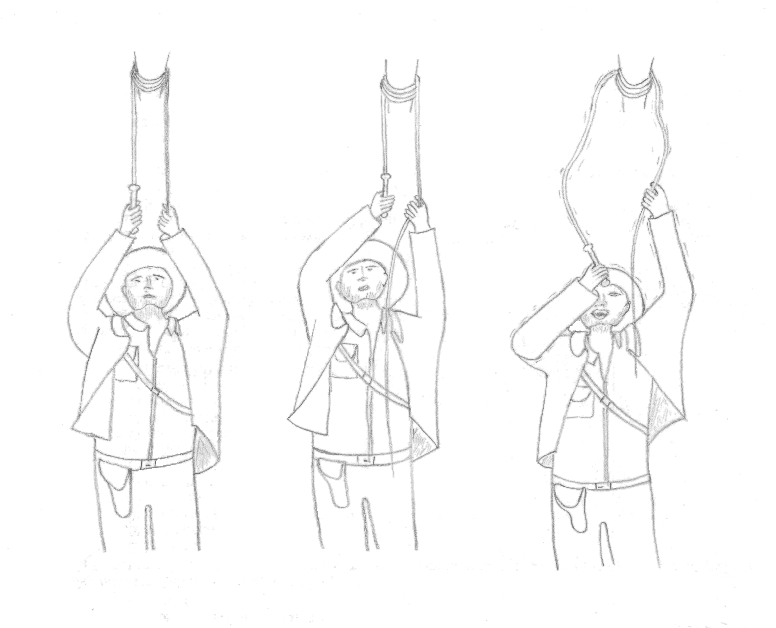
    Lo que se puede generalizar a una sección cualquiera tomando  el perímetro l de una vuelta y la fricción media a

δP_M = µl.(n+1/2).d

Precisiones

    Se podría creer que se encontró la solución, pero no es el caso. Es un principio de respuesta que es verdadero en un caso hipotético limitado. Reflexionamos comparando la diferencia de pesos suspendidos a las extremidades. Sin peso, con una extremidad libre, no se pueden suspender sino bajas masas, incluso con numerosas vueltas. La razón se mencionó antes; las fricciones aumentan con la tensión de la cuerda. Ahora bien si hay una gran diferencia de peso, y sobre todo si una de las extremidades es libre, la tensión y las fricciones por este lado serán escasas, lo que no permitirá compensar el peso del otro lado. Es decir, la tensión para retener el peso es proporcional a este peso pues ella no puede ser nula.

Rq: aquí diferencia de tensión en cuestión; PlS, proportionnallité de las tensiones = > hacer appara la tensión (en µ)

    En la práctica, es necesario al menos una mazarota (el peso de la cuerda no basta) y una diferencia de peso del orden de las masas colgadas.

    La explicación es la siguiente: se dijo que las fricciones étainet sólidos. Eso significa que se puede ejercer una fuerza sin que la cuerda se mueva mientras no supere un determinado valor. Una vez alcanzada ésta, el movimiento tiene lugar. Es lo que permite suspender un peso inferior a este límite.

    Las vueltas tienen pues por objeto reducir la tracción al mínimo pero es necesario siempre oponerle por una fuerza contraria para pasar bajo este límite.

A seguir...

Vuelta al índice