Can Indy cross with its whip?

    In the cave, Indiana Jones is continued by the henchmen of Shiva. It is found wedged by an ignited chasm. It declads sdon whip, warns a beam and fact claquer the whip. This one is rolled up around the beam and our hero in Fedora flies away in the airs and finds on the other side of the chasm, healthy and except. A small jolt and the whip is released.
    In film, Indy is saved because the whip is clutched firmly with the beam. But in would reality, the whip have held? It is what we will see.

Frictions

    Let us start with the beginning. We did everything this experiment to roll up a string around an axis and to draw. And we did everything the same observations: that resists, but that does not hold. And one finds oneself with the string in a hand, the axis in the other.

    One falls already on this report: if ever Indy were hung with its whip, our adventurer is by ground! You will say to me, a this history, why divide the strings in four? And well if the string does not hold, a resistance was nevertheless smelled. There is thus a hope, a possibility that Indy passes on other side or at least which it holds until there.

    What does it thus occur when one rolls up the string so that a resistance is felt? The answer is very simple. There is friction (solid) graft the cord and its support (the axis). Simplest to realize it is to make the following experiment; to pass a cord to horse on a support, preferably rugeux and broad, to attach to it to height equalize equal masses. Is the whole in balance what is normal since the support plays here the part of a pulley? If one adds to the one of the weights a little weight, at one time the équlibre will be broken and twists it and the weights will slip. But in this interval of weight, balance is maintained in spite of the difference in weight. That is due to the friction of the cord on the support. With a pulley this friction would be non-existent and the cord would rock.

    One can use this experiment besides to measure the coefficient of friction of the cord on his support.

    Friction along the half rolls higher compensates for the difference in weight limiting, that is to say,

δP_max = π.r.µ

where µ is the coefficient of friction. It depends naturally on the nature of the support and of the cord, the cord will slip more easily on a steel bar than on a branch or if it is out of nylon rather than in hemp. The pressure or the tension also plays a part. On a suface planes of comparable nature that the axis (support), the cord will slip less if one appuye above. On a curved surface the tension of the cord has the same effect because it will tend to draw the cord towards the axis from the support, therefore to press it against.

    Thus a cord supporting two important weights will slip under an excess of weight more important than a free cord of weight).

    Now that better the origin of this resistance is included/understood, one sees there more clearly on the means of putting it in œuvre to make cross our hero. Let us look further into this friction first of all.

    How could we optimize this friction? If you read well what precedes, you already have at the head the two means. It is a question either of increasing the coefficient of friction, or that frictions take place on more cord. As it is out of question of changing its support, one can forget all that is referred to it (size, nature...). One can on the other hand act over the nature of the cord and the length of cord working.

      

Optimizations

    Let us take whips of different nature: a cord, rubber and a thin strap or a strap. The cord will be used to us as witness to compare.

    Each one knows that rubber adheres better than the cord or leather. That means that it has a coefficient of friction higher than that of the cord. According to the formula found higher, that means that the difference in weight between the two bits which the cord by frictions can compensate for will be higher with rubber than with a normal core.

    Another means of increasing adherence is to increase the syrface in contact; it is very simple to include/understand, by imagining that Indy does not use one but two whips eb parallel: surface in contact with the support will be doubled and our difference in weight supported will be double. That would amount having a coefficient of double friction, 2µ. It is more correct to add a factur which holds account length of the cord in contact (diameter for a cylindrical cord, width for a strap).

δP_M = µ.r.d.π

    The preceding example of two cords coast at coast suggests another optimization. Instead of taking several cords or a cord of higher diameter, why not use the same cord and again make it pass to the top of the support one, two or several times! By holding all the loops at the same time, there will be the equivalent.

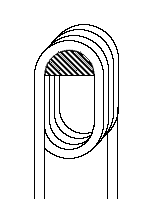
δP_M = µ.r.n.d.π

    Obviously, that is hardly practical and a better solution exists. It is obvious: to roll up the cord on the support so that it is to the maximum in contact  with each turn, and to exert the forces on the ends. If N is the complete number of turns, on a cylindrical component, one has with the additional half turn

δP_M = µ.2π.r.(n+1/2).d

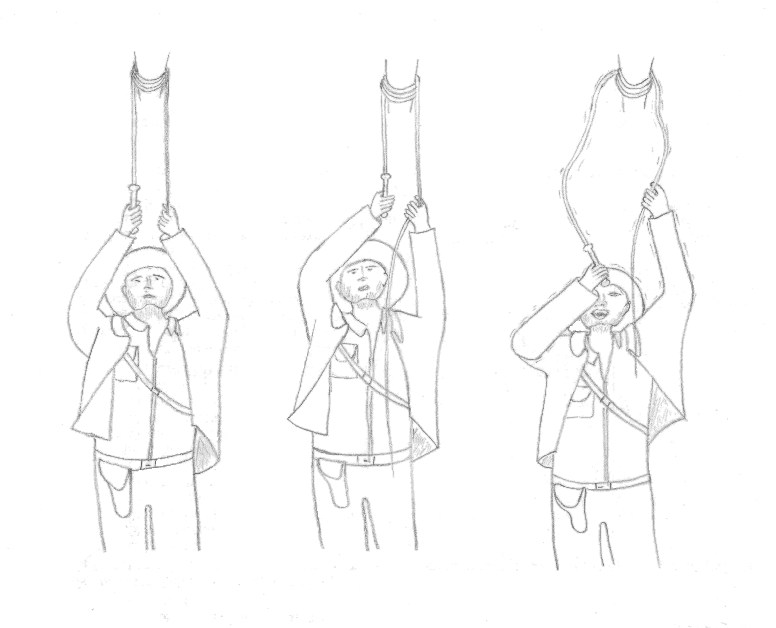
    What one can generalize with an unspecified section by taking  the perimeter L of a turn and average friction with

δP_M = µl.(n+1/2).d

Specified

    One could believe that the solution was found, but it of it is nothing. It is a beginning of answer which is true in a limited case of figure. We reflected by comparing the difference in weights suspended at the ends. Without weight, with a loose lead, one can suspend only low masses, even with many turns. The reason was evoked earlier; frictions increase with the tension of the cord. However if there is a great difference in weight, and especially if one of the ends is free, the tension and frictions on this side will be weak, which will not make it possible to compensate for the weight on other side. In other words, the tension to retain the weight is proportional to this weight thus it cannot be null.

Rq: here difference in tension considered; PlS, proportionnallity of the tensions = > to make apparaitre the tension (in µ)

    In practice, one needs at least a runner (the weight of the cord is not enough) and a difference in weight of the order of the hung masses.

    The explanation is as follows: it was said that solid frictions étainet. That means that one can exert a force without the cord not moving as much as it does not exceed a certain value. Once this one reached, the movement takes place. It is what makes it possible to suspend a weight lower than this limit.

    The purpose of the turns are thus to reduce traction to the minimum but it always should be opposed by a contrary force to pass under this limit.

To follow...

Return to the index